Many problems within polygon algorithms can be solved by partitioning the
polygon into convex parts and solving it for these instead. Even more strict
some solutions require working on a triangle partition (which is easily
constructed from a convex polygon). partition_convex() provides two
algorithms for convex partitioning of polygons with the option to further
partition the convex parts into triangles. The optimal algorithm ensures the
minimum number of resulting partitions at the expense of memory (O(n^3)) and
time (O(n^4)) cost with n being the number of vertices in the polygon.
Alternatively the non-optimal algorithm is much faster (O(n log n)) and
produces at most 4 times the number of partitions that the optimal would.
Another class of partition is one that produces y-monotone polygons, that is,
polygons that are formed by two y-monotone polylines. This partition type is
provided by partition_monotone().
Arguments
- x
A
polyclid_polygonvector- optimal
Should the optimal algorithm be used
- triangulate
Should the convex partition further be partitioned into triangles
Examples
poly <- polygon(
c(391, 240, 252, 374, 289, 134, 68, 154, 161, 435, 208, 295, 421, 441),
c(374, 431, 340, 320, 214, 390, 186, 259, 107, 108, 148, 160, 212, 303)
)
plot(poly)
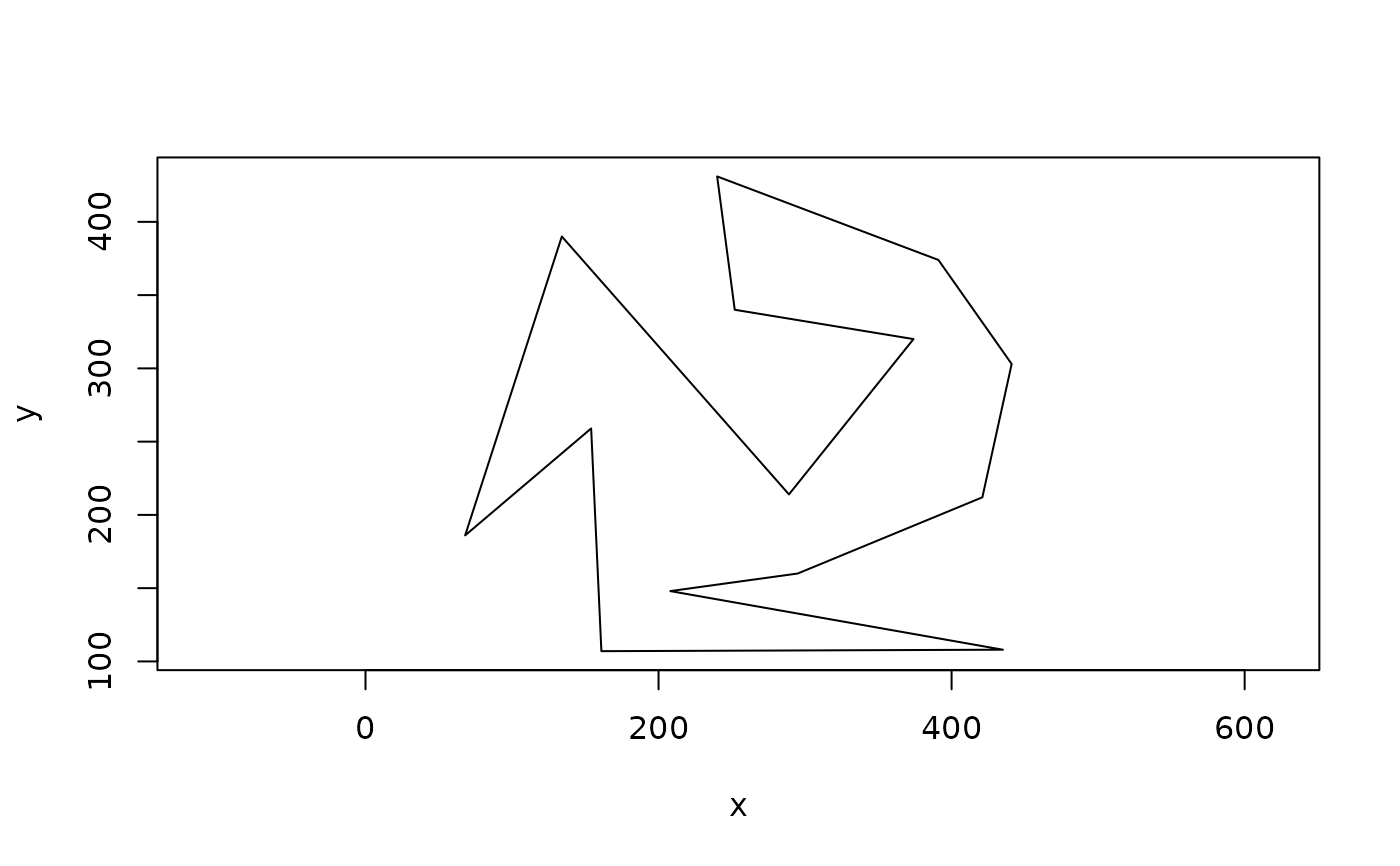 # Optimal
plot(partition_convex(poly, optimal = TRUE))
# Optimal
plot(partition_convex(poly, optimal = TRUE))
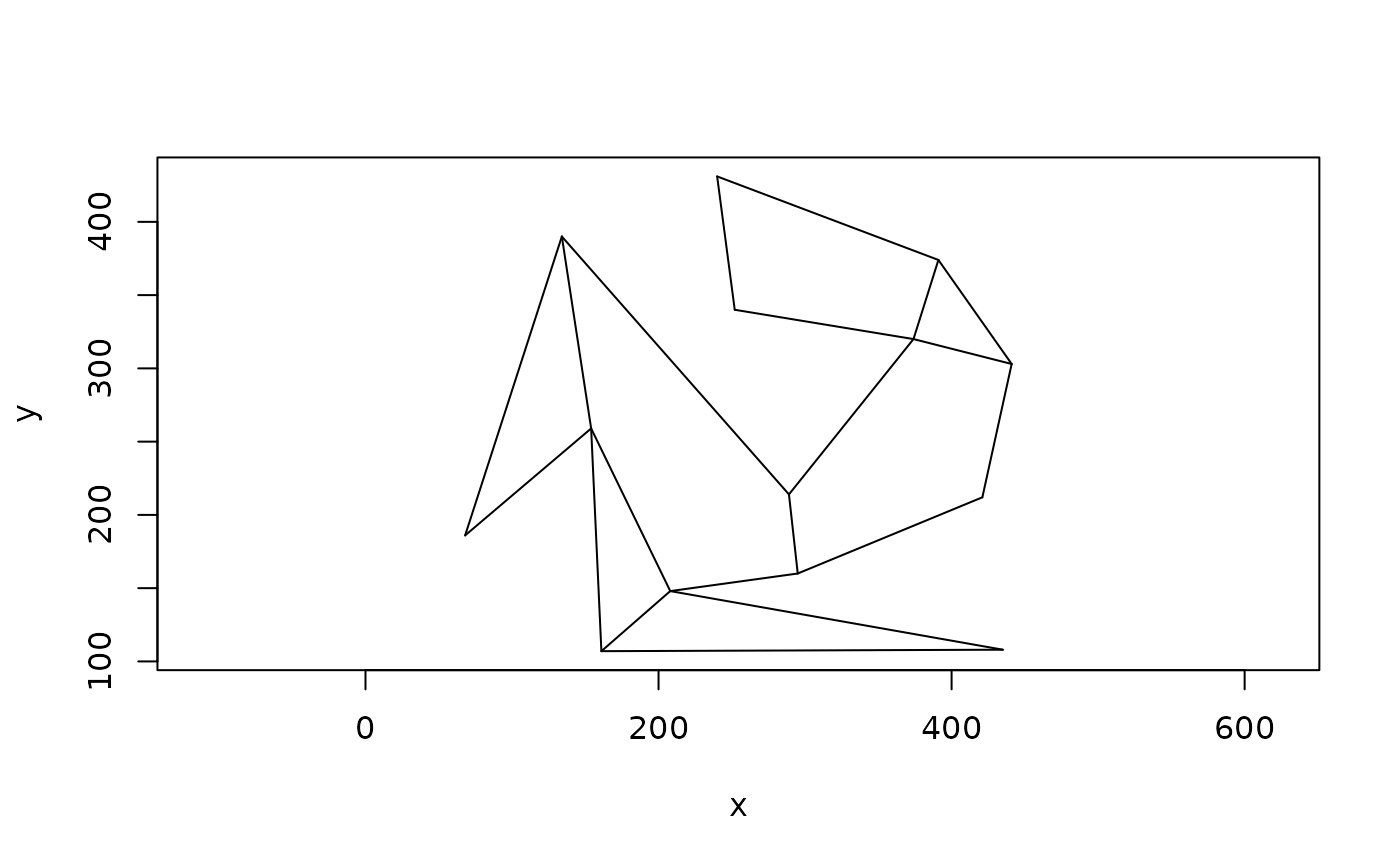 # Approx (no obvious quality degradation in this case)
plot(partition_convex(poly))
# Approx (no obvious quality degradation in this case)
plot(partition_convex(poly))
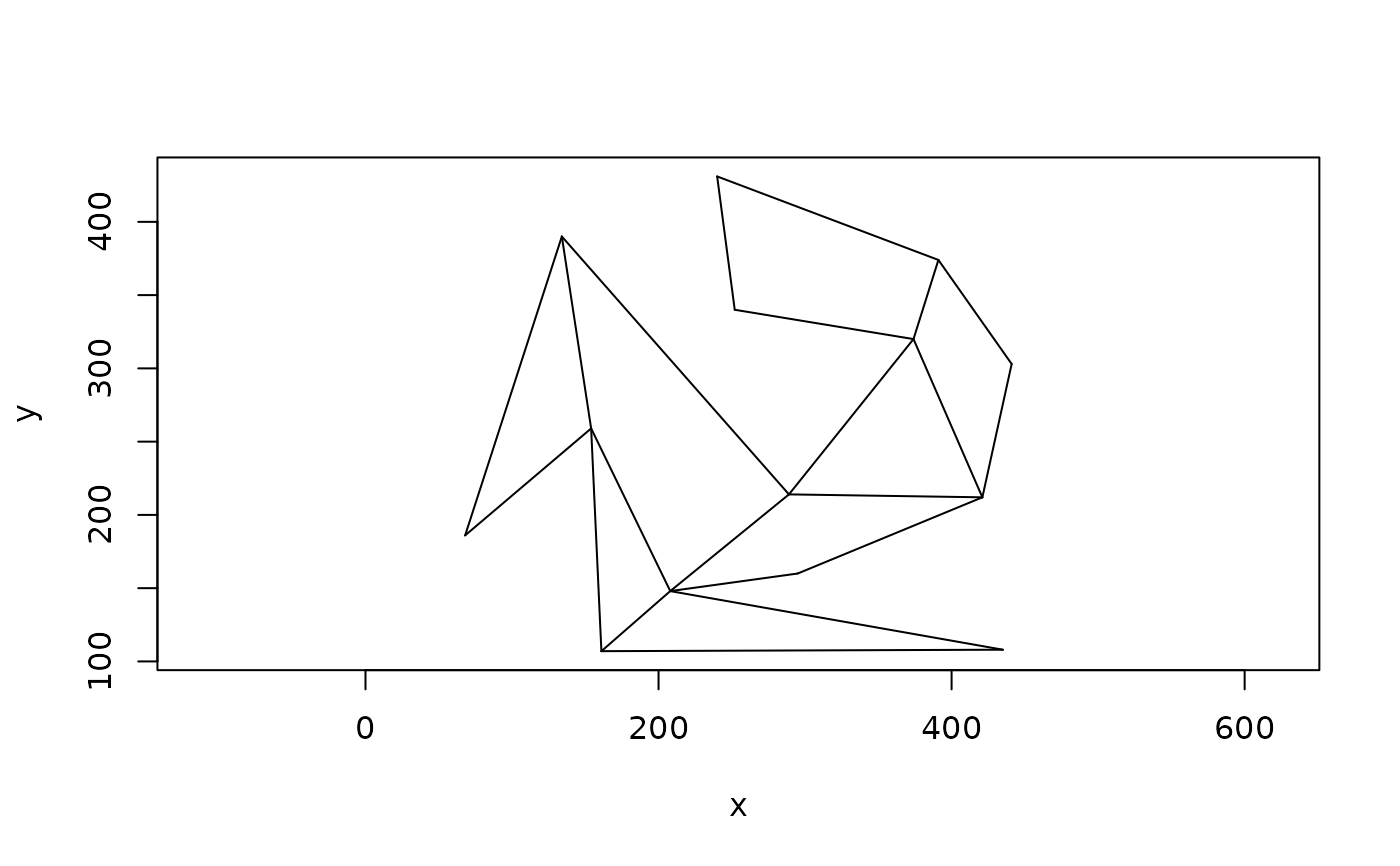 # Triangulate the resulting partitions
plot(partition_convex(poly, triangulate = TRUE))
# Triangulate the resulting partitions
plot(partition_convex(poly, triangulate = TRUE))
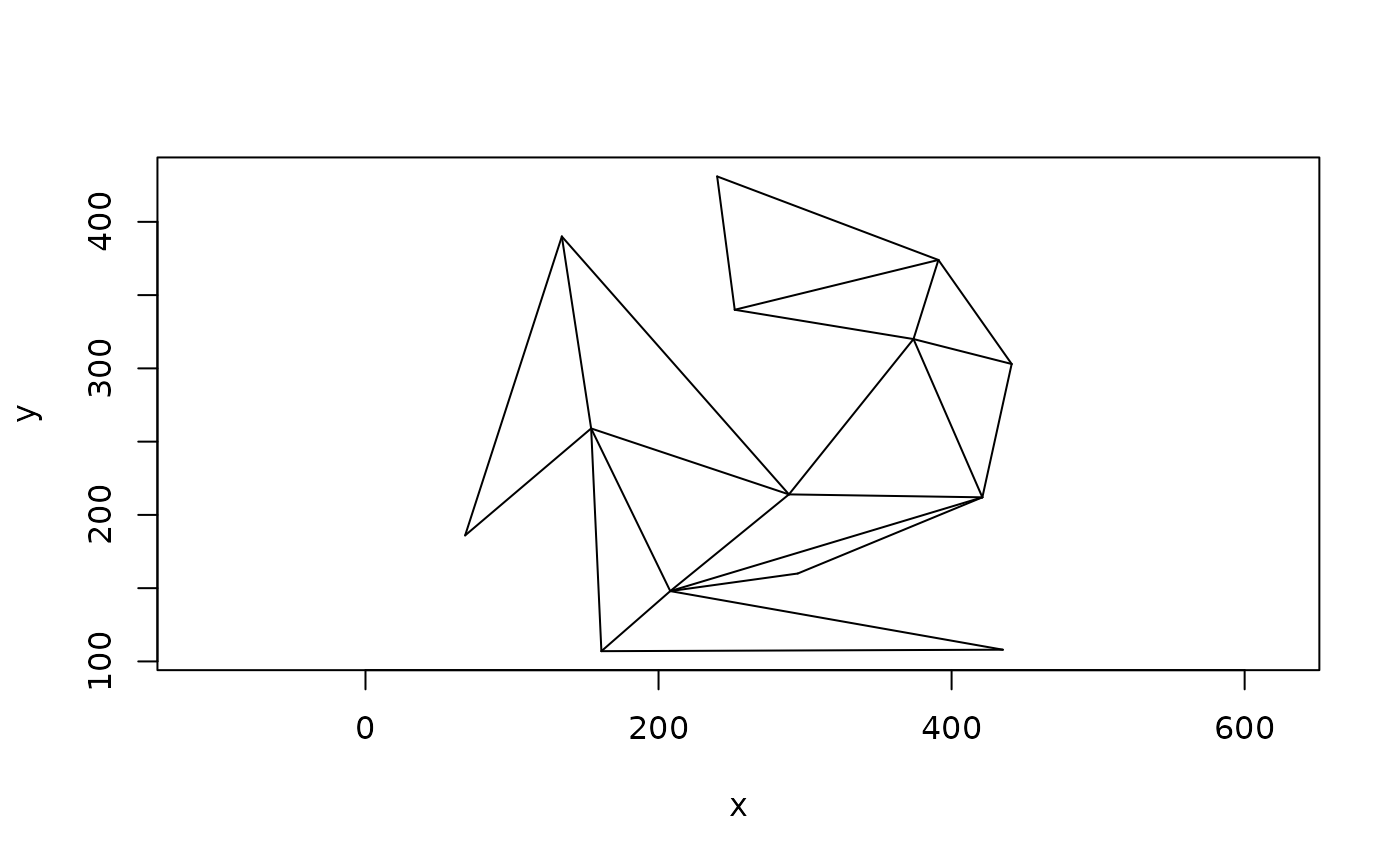 # Do a monotone partition
plot(partition_monotone(poly))
# Do a monotone partition
plot(partition_monotone(poly))
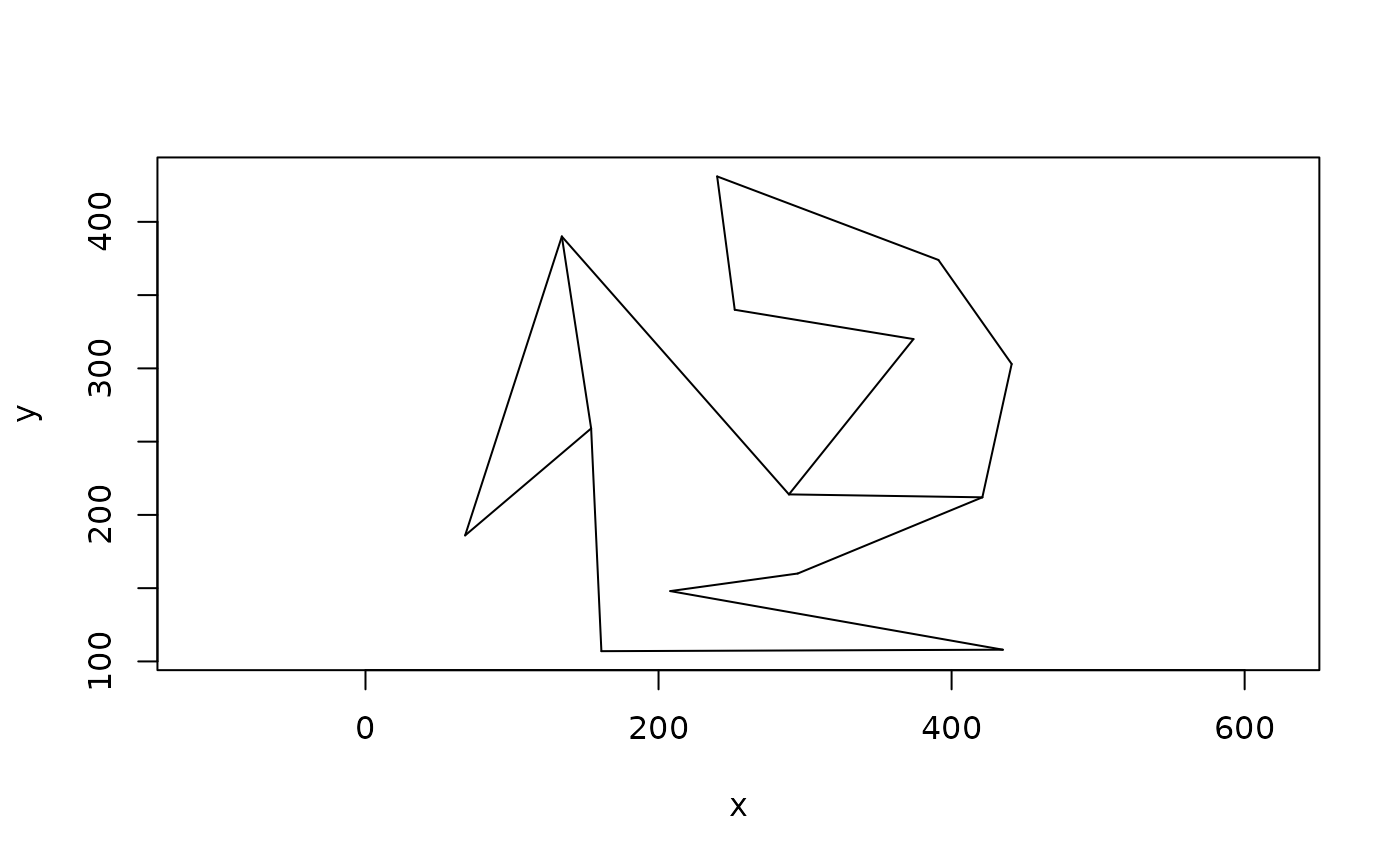 # If you want to work on the polygons further you convert it to a polygon vector
as_polygon(partition_monotone(poly))
#> <2D polyclid_polygons [3]>
#> [1] [Boundary: 3, Range: <<68, 186>, <154, 390>>, Holes: 0]
#> [2] [Boundary: 8, Range: <<134, 107>, <435, 390>>, Holes: 0]
#> [3] [Boundary: 7, Range: <<240, 212>, <441, 431>>, Holes: 0]
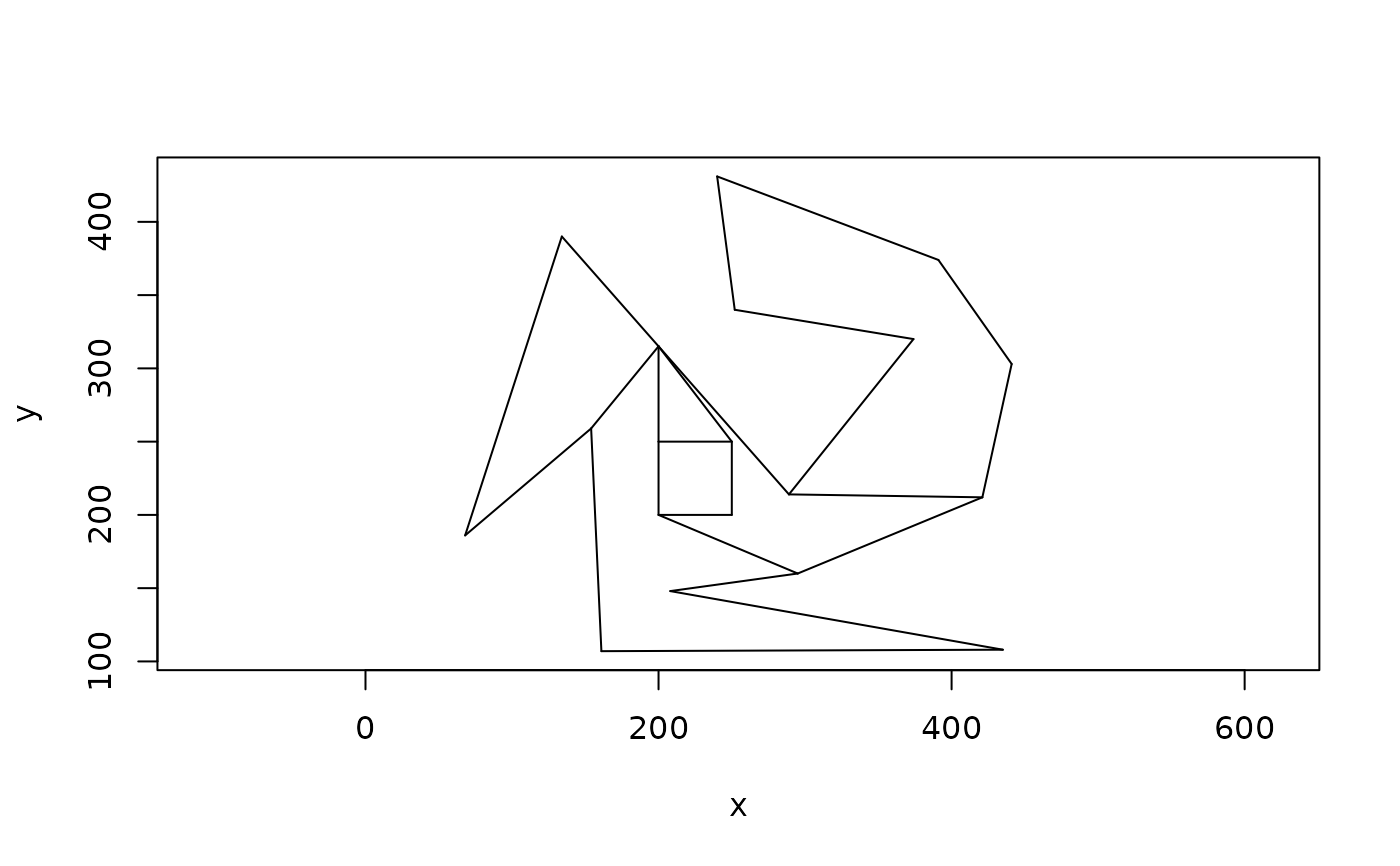
# If the polygon contains holes new vertices may get introduced as those are
# connected to the outer boundary first using `connect_holes()`
hole(poly) <- iso_rect(point(200, 200), point(250, 250))
plot(partition_monotone(poly))
# If you want to work on the polygons further you convert it to a polygon vector
as_polygon(partition_monotone(poly))
#> <2D polyclid_polygons [3]>
#> [1] [Boundary: 3, Range: <<68, 186>, <154, 390>>, Holes: 0]
#> [2] [Boundary: 8, Range: <<134, 107>, <435, 390>>, Holes: 0]
#> [3] [Boundary: 7, Range: <<240, 212>, <441, 431>>, Holes: 0]
# If the polygon contains holes new vertices may get introduced as those are
# connected to the outer boundary first using `connect_holes()`
hole(poly) <- iso_rect(point(200, 200), point(250, 250))
plot(partition_monotone(poly))
 # Use `ignore_inner = TRUE` to avoid extracting holes from a partition
res_with_hole <- as_polygon(partition_monotone(poly))
plot(res_with_hole, col = palette())
# Use `ignore_inner = TRUE` to avoid extracting holes from a partition
res_with_hole <- as_polygon(partition_monotone(poly))
plot(res_with_hole, col = palette())
