Calculate vertex normals of a polyline or polygon

This function allows you to retrieve the vertex normals (mean of normals from the adjacent line segments). As this requires normalising the normals it cannot be done exactle hence the approx_ prefix. For polylines the normal is oriented in the same way as it is for the individual segments, whereas for polygons they are oriented outwards assuming a valid polygon.

Usage

approx_vert_normal(x, ...)

# S3 method for polyclid_polyline
approx_vert_normal(x, ...)

# S3 method for polyclid_polygon
approx_vert_normal(x, ...)

Arguments

x

A polyclid_polyline or polyclid_polygon vector

...

Arguments passed on to methods

Value

A euclid_direction2 vector of normals matchng the vertices returned by euclid::vert()

Examples

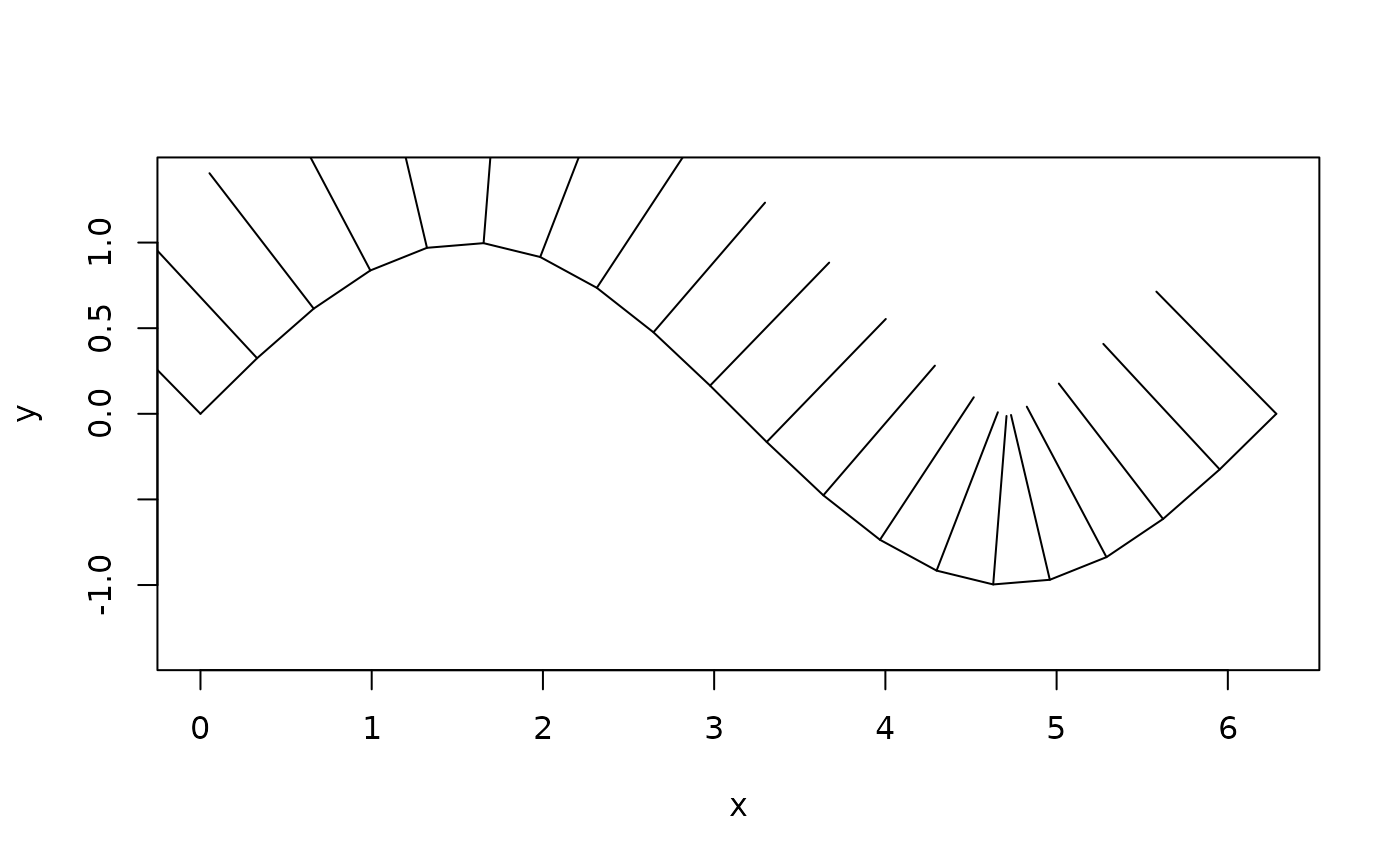
# Polylines
sine <- polyline(
  seq(0, 2*pi, length.out = 20),
  sin(seq(0, 2*pi, length.out = 20))
)
normals <- approx_vert_normal(sine)
normals
#> <2D directions [20]>
#>  [1] <dx:-0.701, dy:0.714> <dx:-0.68, dy:0.733>  <dx:-0.609, dy:0.791>
#>  [4] <dx:-0.465, dy:0.879> <dx:-0.227, dy:0.963> <dx:0.0777, dy:0.984>
#>  [7] <dx:0.358, dy:0.925>  <dx:0.548, dy:0.832>  <dx:0.652, dy:0.757> 
#> [10] <dx:0.695, dy:0.718>  <dx:0.695, dy:0.718>  <dx:0.652, dy:0.757> 
#> [13] <dx:0.548, dy:0.832>  <dx:0.358, dy:0.925>  <dx:0.0777, dy:0.984>
#> [16] <dx:-0.227, dy:0.963> <dx:-0.465, dy:0.879> <dx:-0.609, dy:0.791>
#> [19] <dx:-0.68, dy:0.733>  <dx:-0.701, dy:0.714>

plot(sine)
euclid_plot(segment(vert(sine), as_vec(normals)))


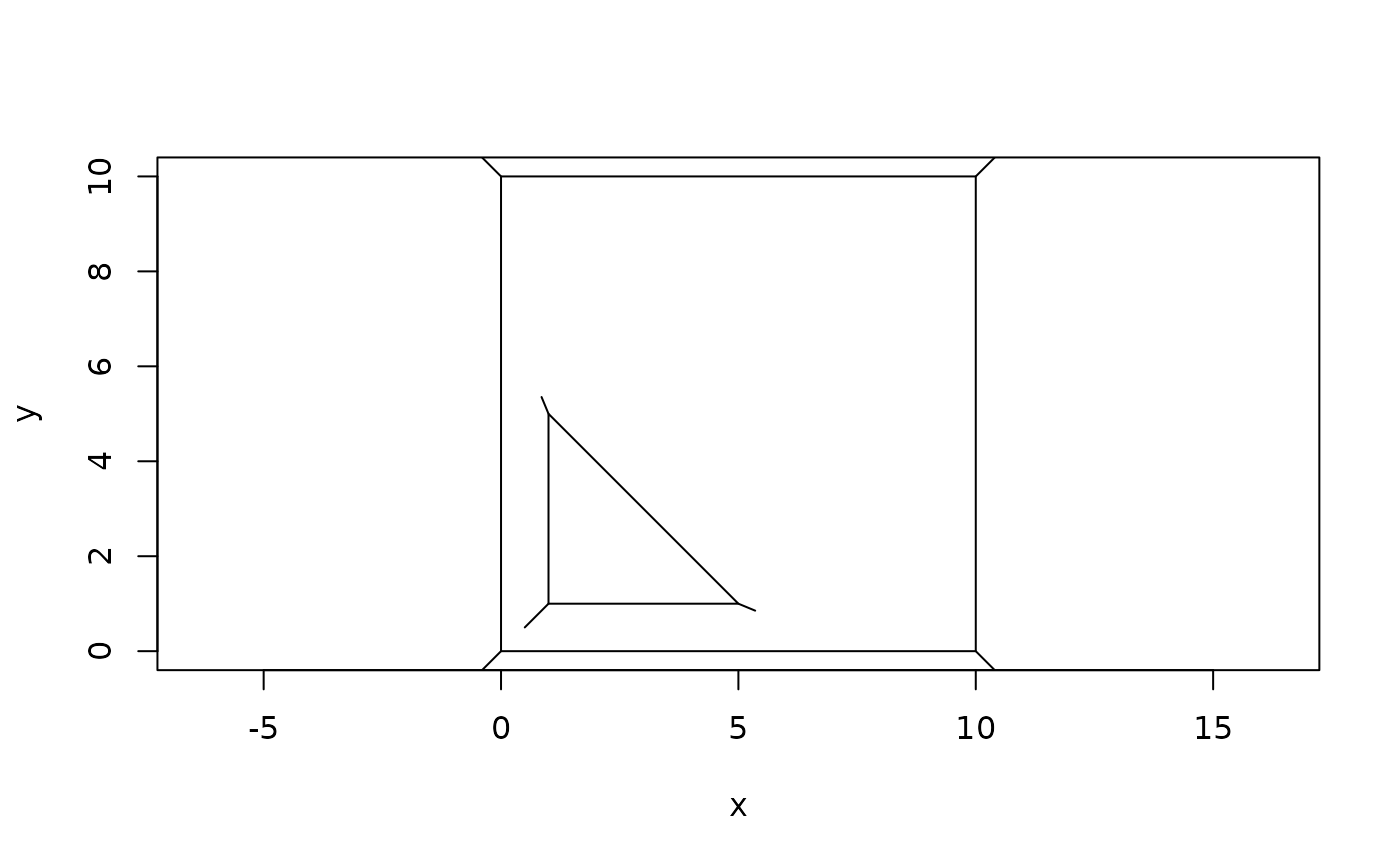
# Polygons
poly <- polygon(
  c(0, 10, 10, 0, 1, 5, 1),
  c(0, 0, 10, 10, 1, 1, 5),
  hole_id = c(1, 1, 1, 1, 2, 2, 2)
)
normals <- approx_vert_normal(poly)
normals
#> <2D directions [7]>
#> [1] <dx:-0.5, dy:-0.5>    <dx:0.5, dy:-0.5>     <dx:0.5, dy:0.5>     
#> [4] <dx:-0.5, dy:0.5>     <dx:-0.5, dy:-0.5>    <dx:0.354, dy:-0.146>
#> [7] <dx:-0.146, dy:0.354>

plot(poly)
euclid_plot(segment(vert(poly), as_vec(normals)))